Navigating the Future: A Comparative Analysis of Trajectory Prediction Models
Trajectory prediction is a challenging task due to the multimodal nature of human behavior and the complexity in multi-agent systems. In this technical report we explore three machine learning approaches that aim to tackle these challenges: Social GAN, Social-STGCNN, and EvolveGraph. Social GAN uses variety loss to generate diverse trajectories and a pooling module to model subtle social cues. Social-STGCNN models social interactions explicitly through a graphical structure. EvolveGraph establishes a framework for forecasting the evolution of the interaction graph. We compare the advantages and disadvantages of these approaches at the end of the report.
Introduction
Trajectory prediction involves assessing the future motion of agents in a scene based on their past trajectories. One of the applications for trajectory prediction is to aid trajectory planning in autonomous vehicles. A significant difficulty in trajectory prediction comes from the fact that agent behavior is multimodal: common past trajectories under different scenarios can lead to different future trajectories.
In general, there are two levels of abstraction in trajectory prediction. At the higher level, the goal is to identify the overall intention of each agent to predict their future behavior. At the lower level, we need to predict the actual continuous trajectories based on physics.
A more descriptive problem statement is as follows: With access to real-time data from sensors, such as LiDAR, radar, and camera, a functioning system that allows detection and tracking of agents, and past positions of agents represented in ego car-centric coordinate system as input, generate the future trajectory of each agent. Formally, based on past trajectories \(X^i = \{ X^i_1, X^i_2, \dots, X^i_{T_{obs}} \}\) at observation times \(t \in \{ 1, 2, \dots, T_{obs} \}\) for all agents \(i\), estimate future trajectories \(\hat Y^i = \{ \hat y^i_{T_{obs} + 1}, \hat y^i_{T_{obs} + 2}, \dots\hat y^i_{T_{pred}} \}\) of all agents [1].
Datasets
Datasets for trajectory prediction can be classified by the type of agent being predicted.
Two especially important datasets for pedestrian trajectory prediction are the ETH [2] and UCY [3] datasets. The ETH dataset consists of 1804 images, separated into three video clips, captured from a car-mounted stereo camera. Meanwhile, the UCY dataset consists of camera footage over 2 scenes that in total have 786 pedestrians. Each of these datasets cover situations with complicated group dynamics (couples holding hands, groups congregating together, etc) in crowded real-world settings.
Meanwhile, datasets for autonomous vehicle trajectory prediction include the nuScenes [4] and Honda 3D (H3D) [5] datasets. These datasets often include multi-modal data. For example, the nuScenes dataset has over 1000 driving scenes with bounding-box ground truths and inputs from camera, radar, and LiDAR.
Methods
Social GAN [6]
Overview
The authors identified three inherent properties of human motion in crowded scenes that pose challenges to human behavior forecasting:
-
Interpersonal. Humans have the innate ability to read the behavior of others when navigating crowds.
-
Socially Acceptable. Pedestrians are governed by social norms such as yielding right-of-way and respecting personal space.
-
Multimodal. Multiple future trajectories are plausible and socially-acceptable.
To tackle these challenges, the authors proposed Social GAN, an RNN Encoder-Decoder generator and an RNN-based encoder discriminator that
-
Introduce a variety loss to encourage the generator to cover the space of possible paths, and
-
Use a new pooling mechanism that encodes subtle social cues for all people in a scene.
Technical Details
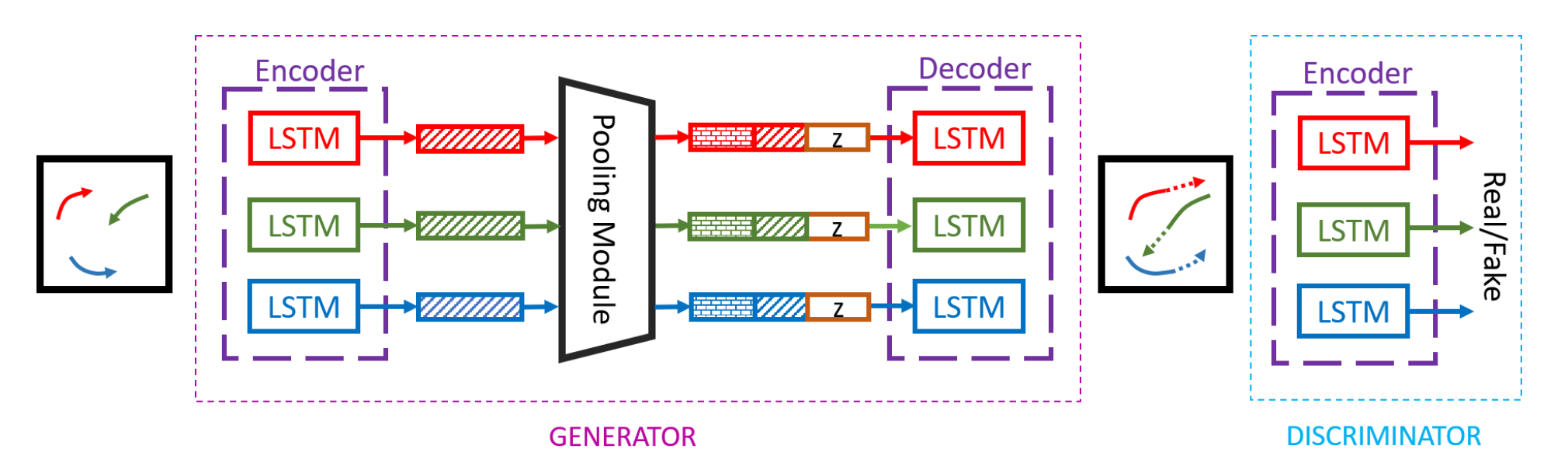
Figure 1. Social GAN architecture overview [1].
Generator: The location of each person is first converted to a fixed-length embedding \(e^t_i\) using a linear layer with ReLU. The embeddings are used as input to LSTM cells that share weights between all people in a scene. Alahi, et al. [7] showed that a compact representation that combines information from different encoders for social interaction reasoning purposes is needed. This is modeled by a Pooling Module that generates a pooled tensor \(P_i\) for each person. The pooled tensor is then passed through an MLP with ReLU nonlinearity to initialize the hidden state of the decoder along with noise.
Pooling Module: For each person \(i\), the relative position of every other person in the scene is computed and concatenated to person \(i\)’s hidden state, processed by an MLP, and pooled elementwise to generate their pooling tensor \(P_i\). It is shown by Qi et al. [8] that by using a symmetric function (Max-Pooling is used in Social GAN), the pooling module is able to address variable and large number of people in a scene, and scattered interaction between far-away pedestrians.
Discriminator: The discriminator consists of a separate encoder that takes as input \(T_{real} = [X_i, Y_i]\) or \(T_{fake} = [X_i, \hat Y_i]\) and classifies them as real or fake by applying an MLP to the encoder’s last hidden state.
Losses. The authors applied \(L_2\) loss on the predicted trajectory to measure distance from ground truth in addition to adversarial loss. The authors also proposed a variety loss function where the model generates \(k\) outputs for each scene and the variety loss chooses the “best” prediction in the \(L_2\) sense as the prediction. This encourages the model to generate diverse trajectories.
Social-STGCNN [9]
Overview
Previous trajectory prediction models have sought to model social interactions between pedestrians via aggregation modules, like with the pooling module in Social GAN. Instead, Social-STGCNN seeks to explicitly model these interactions through a graphical structure. It claims that aggregation layers for social modeling are both unintuitive and indirect, given that the feature space cannot be easily physically interpretable. Aggregation layers also often fail to capture the correct social interactions (for example, pooling layers leak information). Instead, Social-STGCNN proceeds to
-
Explicitly model pedestrian trajectories through a spatial-temporal graph. Edges model the social interaction between pedestrians. Explicitly, this graph can be represented as a weighted adjacency matrix, where each edge weight quantifies the amount of interaction between pedestrians.
-
Manipulate the social interaction graph through a graph convolutional neural network and a temporal convolutional neural network to predict all sequences in a single shot.
Technical Details
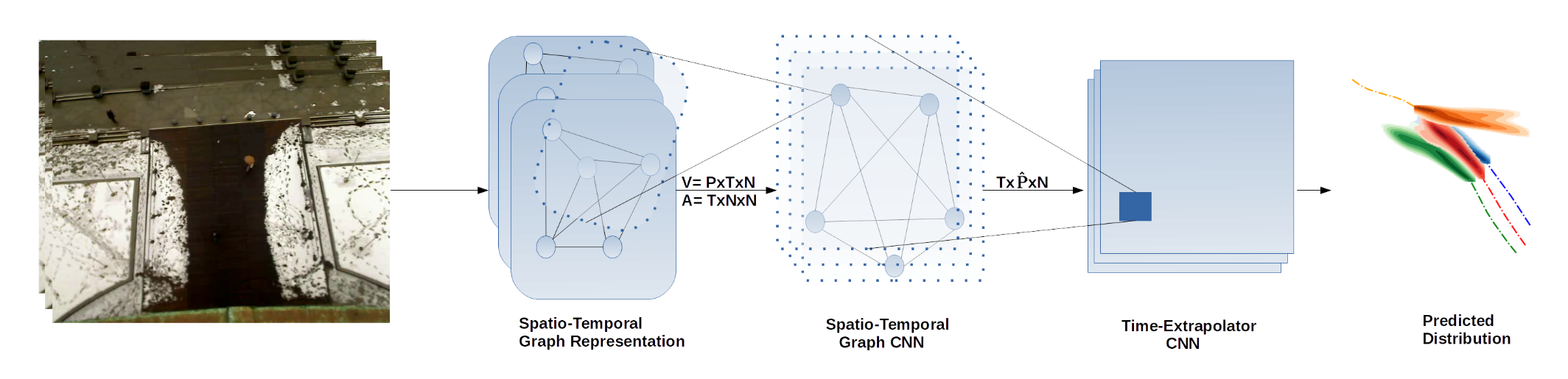
Figure 3. The Social-STGCNN model [9].
Social-STGCNN makes the assumption that each of the pedestrian trajectories can be assumed to have been sampled from a bivariate Gaussian normal distribution. Thus, for each pedestrian \(n\) and time \(t\), Social-STGCNN predicts a mean \(\mu_t^n\), a variance \(\sigma_t^n\), and correlations \(p_t^n\) for the bivariate Guassian. For each ground-truth label, the model aims to minimize the negative log-likelihood loss of that ground-truth label occurring.
The model itself consists of two distinct parts: the Spatio-Temporal Graph CNN (ST-GCNN) and the Time-Extrapolator CNN (TXP-CNN). ST-GCNN extracts features from the graph representation and TXP-CNN uses these features to predict the future trajectories of all pedestrians.
First, the model builds the spatio-temporal graph representation as a set of spatial graphs \(G_t\) for each time step \(t\). Each pedestrian \(i\) at the time step \(t\) is represented by a vertex \(v_t^i\) with its attributes being the observed position \((x_t^i, y_t^i)\). Then, to compute the edge weight between the vertices \(v_t^i\) and \(v_t^j\) through a kernel function that takes the inverse of the norm of \((x_t^i-x_t^j, y_t^i - y_t^j)\).
Secondly, the model uses ST-GCNN to extract features from this graph. In a normal spatial graph convolution, the convolution for a single vertex \(v^i\) is instead computed over a set of neighboring vertices (a neighboring vertex is one whose shortest path to \(v^i\) is less than some distance \(D\)). This stands in contrast to a normal convolution layer, where the convolution is calculated instead of over an entire 2D kernel. ST-GCNN extends normal spatial graph convolution by incorporating temporal information as well. Thus, it better encodes features of a spatio-temporal trajectory. The ST-GCNN ultimately creates a graph embedding \(\overline{V}\).
Then, the Time-Extrapolator CNN (TXP-CNN) operates directly on the temporal dimension of the graph embedding \(\overline{V}\). It then expands this dimension with temporal convolutions as necessary to create a trajectory prediction for each pedestrian. Since the TXP-CNN operates on the feature space, it manages to have far fewer parameters than recurrent units. Moreover, an interesting property to note is that the model output will be invariant to the initial ordering of pedestrians in the data.
EvolveGraph [10]
Overview
EvolveGraph seeks to model multi-agent interacting systems in a dynamically changing system over time, which is a key aspect of trajectory prediction. One key advancement that EvolveGraph provides is, as the name implies, the ability of the interaction graph to evolve over time. Most models leading up to EvolveGraph would generally model interactions as a static set of edges between agents, but EvolveGraph is able to adapt the underlying interaction graph over time, which allows it to capture more complex interaction patterns between agents to improve upon the prediction accuracy.
In order to support this graph, the authors also introduce a custom forecasting framework. This framework can incorporate trajectory information and context information (such as scene images or semantic maps) in order to accurately capture the multi-modality of future states too.
Technical Details
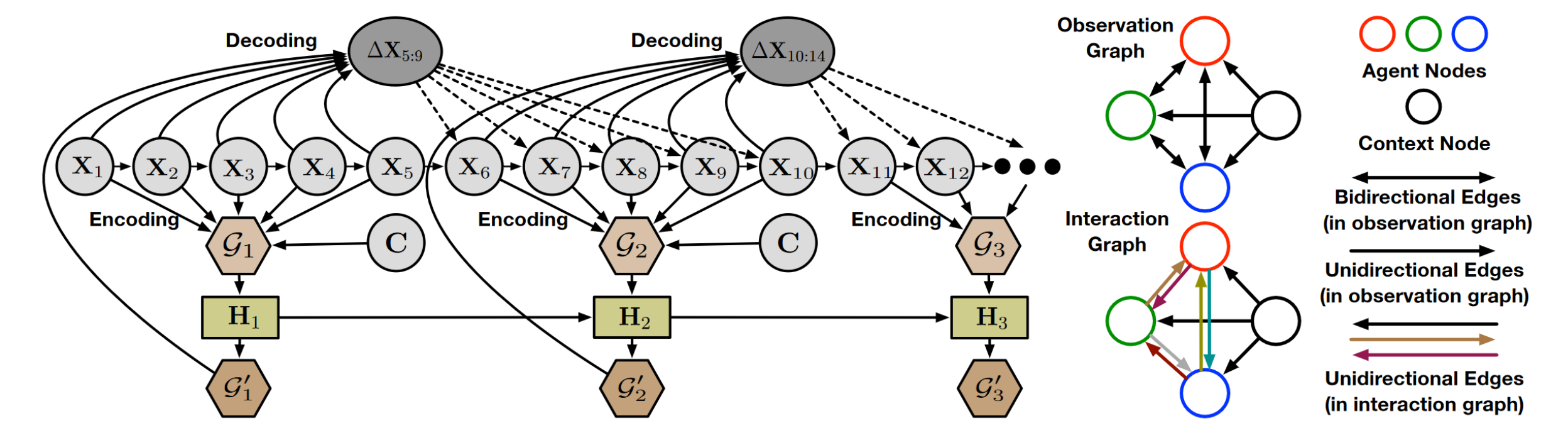
Figure 2. High level approach of EvolveGraph [10].
The high level approach of EvolveGraph can be seen above. Since the graph needs to evolve over time to capture new agent interactions, an encoder and decoder system is used to regenerate new graphs after some amount of time steps (which is 5 in the above example). By using the states of the actors at certain time steps and the contest of the environment, the model is able to recompute a latent representation of the interaction graph to be used for future trajectory prediction. This forms the static interaction graph prediction. The network then combines the static graph with the graph from the previous set of timesteps to form a dynamic interaction graph, learned on a recurrent network.
For the static graph portion, each agent is assigned two components: a self attribute that indicates its own state, and a social attribute that indicates the state of the environment. Each edge is calculated using learnable attention parameters that emphasize what other agents the current agent should give more weight to when determining trajectory.
For the dynamic graph portion, the encoding process is repeated every \(\tau\) time steps. Since the graph should be dependent on the previous graphs, a gated recurrent unit (GRU) is used to store previous graph information and pass it forward to predict the new graph.
In order to train this network, the authors first train the encoding/decoding network using the static interaction graphs. Once the encoder/decoder is trained, the authors are then able to train the dynamic interaction graph since this is based on the latent representation of the interaction graph. Interestingly, the authors found that training the dynamic interaction graph directly leads to a large convergence time since there are far too many parameters to train on it directly [10].
Results

Figure 4. Comparing Social-STGCNN and Social GAN (sgan) models qualitatively [9].
In 2020, the Social-STGCNN was compared to the performance of several prediction models on the pedestrian ETH and UCY datasets. Ultimately, Social-STGCNN had an Average Displacement Error (ADE) of 0.44 and Final Displacement Error (FDE) of 0.75 compared to Social GAN’s ADE of 0.61 and FDE of 1.21. It accomplished these significantly better results while having much faster inference time and also using far fewer parameters. Social GAN has 46.3k parameters and an inference time of 0.0968s, while Social-STGCNN has 7.6k parameters (6.1× better) and an inference time of 0.0020s (48.4× better). As shown qualitatively below, when sampling on several scenes, the Social-STGCNN was better at tracking the ground truth in comparison to Social GAN.
| Social GAN | Social-STGCNN | EvolveGraph | |
|---|---|---|---|
| H3D (4.0s) | 0.94 / 1.91 | 0.73 / 1.49 | 0.48 / 0.86 |
| NBA (4.0s) | 3.60 / 6.24 | 2.35 / 3.71 | 1.83 / 3.16 |
| SDD (4.8s) | 27.0 / 43.9 | 20.6 / 36.4 | 13.9 / 22.9 |
Table 1. minADE20 / minFDE20 (Meters) of trajectory prediction on different datasets [10].
EvolveGraph Performance was compared against several state-of-the-art trajectory prediction models, including Social-GAN And Social-STGCNN on traffic, basketball, and university datasets (H3D, NBA, and SDD). The results showed that EvolveGraph consistently was 20-30% more accurate than any of its counterparts.
Table 1 shows the evaluation results on each of these datasets. The performance is measured in terms of two widely used standard metrics: minimum average displacement error (minADE20) and minimum final displacement error (minFDE20). The minADE20 is defined as the minimum average distance between the 20 predicted trajectories and the ground truth over all the involved entities within the prediction horizon. The minFDE20 is defined as the minimum deviated distance of 20 predicted trajectories at the last predicted time step.
Discussion
Generally speaking, the performance of a model is contingent on how well that model is able to represent the social interactions between pedestrians. As an initial starting point, Social GAN captures social interactions through pooling layers. However, these pooling layers are hard to intuitively understand and may end up actually losing information. Thus, Social-STGCNN introduces an explicit representation of pedestrian interaction by constructing a spatio-temporal graph. This new representation corresponds to Social-STGCNN performing better. Finally, EvolveGraph can learn a dynamic interaction graph (whereas the Social-STGCNN’s interaction graph is static), which improves the ability of this model to represent trajectory prediction.
Each model has a unique strength when it comes to its effectiveness for trajectory prediction. Social GAN is particularly useful in producing globally coherent and socially compliant diverse samples. Meanwhile, Social-STGCNN is a highly efficient approach that offers an explicit representation and intuitive understanding of social interactions. Finally, EvolveGraph provides explicit relational reasoning among multiple heterogeneous, interactive agents with a graph representation. Additionally, its dynamic mechanism allows it to evolve the interaction graph, leading to a highly competitive performance in comparison to the other three models. By utilizing these different techniques, researchers can predict the trajectories of different actors in an environment depending on what the specific situation calls for.
However, each of these models has its drawbacks compared to one another. According to the Social-STGCNN authors, the aggregation layers that Social-GAN uses for social modeling are unintuitive and indirect. Additionally, many recurrent nodes mean that this network ends up being very slow compared to CNN architectures. While Social-SGTCNN improves upon the speed, the tradeoff here is that stacking the ST-GCNN layers can lead to vanishing gradients, which would result in worse performance for deeper networks. Finally, EvolveGraph suffers from a similar problem to Social-GAN, where the recurrent nodes combined with many parameters can lead to a slower convergence.
Reference
[1] Leon, F., & Gavrilescu, M. (2021). A Review of Tracking and Trajectory Prediction Methods for Autonomous Driving. Mathematics, 9(6).
[2] Pellegrini, L. (2010). Improving Data Association by Joint Modeling of Pedestrian Trajectories and Groupings. In Computer Vision – ECCV 2010 (pp. 452–465). Springer Berlin Heidelberg.
[3] Leal-Taixé, L., Fenzi, M., Kuznetsova, A., Rosenhahn, B., & Savarese, S. (2014). Learning an Image-Based Motion Context for Multiple People Tracking. In 2014 IEEE Conference on Computer Vision and Pattern Recognition (pp. 3542-3549).
[4] Holger Caesar, Varun Bankiti, Alex H. Lang, Sourabh Vora, Venice Erin Liong, Qiang Xu, Anush Krishnan, Yu Pan, Giancarlo Baldan, & Oscar Beijbom (2020). nuScenes: A multimodal dataset for autonomous driving. In CVPR.
[5] Abhishek Patil, Srikanth Malla, Haiming Gang, & Yi-Ting Chen (2019). The H3D Dataset for Full-Surround 3D Multi-Object Detection and Tracking in Crowded Urban Scenes. In International Conference on Robotics and Automation.
[6] Gupta, A., Johnson, J., Fei-Fei, L., Savarese, S., & Alahi, A. (2018). Social GAN: Socially Acceptable Trajectories with Generative Adversarial Networks. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR).
[7] Alahi, A., Goel, K., Ramanathan, V., Robicquet, A., Fei-Fei, L., & Savarese, S. (2016). Social LSTM: Human Trajectory Prediction in Crowded Spaces. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (pp. 961-971).
[8] Qi, C., Su, H., Mo, K., & Guibas, L. (2016). PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. arXiv preprint arXiv:1612.00593.
[9] Mohamed, A., Qian, K., Elhoseiny, M., & Claudel, C. (2020). Social-STGCNN: A Social Spatio-Temporal Graph Convolutional Neural Network for Human Trajectory Prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 14424–14432).
[10] Li, J., Yang, F., Tomizuka, M., & Choi, C. (2020). EvolveGraph: Multi-Agent Trajectory Prediction with Dynamic Relational Reasoning. In Proceedings of the Neural Information Processing Systems (NeurIPS).