Conditional Control of Text-to-Image Diffusion: ControlNet and FreeControl
In the realm of artificial intelligence, the text-to-image(T2I) generation has become a focal point of research. ControlNet stands out by offering users precise spatial control over T2I diffusion models. On the other hand, FreeControl represents a paradigm shift by granting users unparalleled control over T2I generation without the need for extensive training processes. This blog aims to provide an in-depth comparison between ControlNet and FreeControl.
Introduction
In the realm of artificial intelligence, the text-to-image (T2I) generation has emerged as a significant focal point of research. Among the myriad of approaches, ControlNet[1] has distinguished itself by offering users an impressive degree of precision in manipulating spatial aspects within T2I diffusion models. However, this precision is not without its trade-offs. Achieving such fine-tuned control demands the training of auxiliary modules tailored to specific spatial conditions, model architectures, and checkpoints.
In contrast, FreeControl[2] brings a paradigm shift in the field, presenting a novel approach that liberates users from the burden of extensive training processes. It supports multiple control conditions, model architectures, and customized checkpoints without any training while giving unparalleled control over T2I generation.
This blog delves into the depths of these two pioneering technologies, ControlNet and FreeControl, illuminating their architectures and experimental results. However, it’s important to note that this blog assumes readers are familiar with stable diffusion techniques. Through comparison and analysis, we aim to elucidate the strengths, weaknesses, and potential implications of each approach.
ControlNet
ControlNet presents a framework designed to support diverse spatial contexts as additional conditioning factors for Diffusion models, such as Stable Diffusion. It supports various conditions to control Stable Diffusion, including pose estimations, depth maps, canny edges, and sketches.
Architecture
ControlNet has two steps: copy and connect.
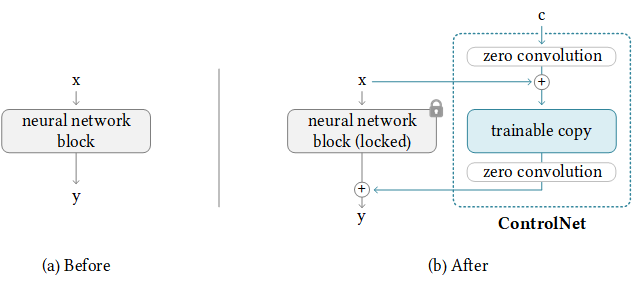
Fig 1. A neural network block with ControlNet [1].
Copy
ControlNet clones the pre-trained parameters of a Diffusion model, such as Stable Diffusion’s latent UNet, resulting in a trainable copy. Additionally, the original pre-trained parameters are preserved separately, referred to as the locked copy. This separation allows the locked copy to retain the extensive knowledge acquired from a large dataset, while the trainable copy is dedicated to learning task-specific features.
Connect
The trainable and locked parameter copies are connected via zero convolution layers, which are optimized within the ControlNet framework. This technique, known as zero convolution, acts as a training mechanism to preserve the semantic knowledge already captured by the frozen model while incorporating new conditions during training.
Now, let’s delve into the equation.
Suppose we have a trained neural block \(F(·; Θ)\) with parameters \(Θ\). An input feature map \(x\) transforms into a feature map \(y\) as \(y = F(x; Θ)\). Adding a ControlNet to this pre-trained neural block involves freezing the parameters \(Θ\) of the original block and simultaneously creating a trainable copy with parameters \(Θ_c\). This trainable copy takes an external conditioning vector \(c\) as input. The trainable copy is connected to the locked model using zero convolution layers, denoted as \(Z(·; ·)\). Specifically, \(Z(·; ·)\) represents a 1 × 1 convolution layer with both weight and bias initialized to zeros. To construct a ControlNet, we utilize two instances of zero convolutions with parameters \(Θ_{z_1}\) and \(Θ_{z_2}\) respectively. The complete ControlNet then computes
\[y_c = F(x; Θ) + Z(F(x + Z(c; Θ_{z_1}); Θc); Θ_{z_2})\], where \(y_c\) represents the output of the ControlNet block.
ControlNet for Text-to-Image Diffusion
This is how ControlNet is added to a diffusion model.
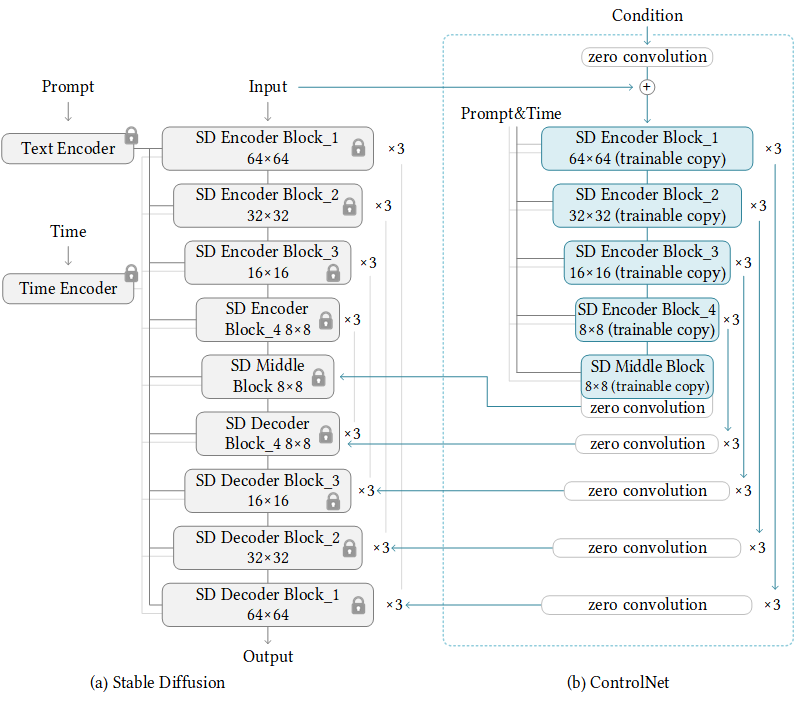
Fig 2. Stable Diffusion’s U-net architecture connected with a ControlNet on the encoder blocks and middle block [1].
ControlNet is connected to each encoder level of the U-net. It can seamlessly be applied to any other model, which is a typical U-net structure. Moreover, it is computationally efficient because only the trainable copy requires training, while the parameters of the locked copy remain frozen.
Training
Given an input image \(z_0\), image diffusion algorithms progressively add noise to the image, resulting in a noisy image \(z_t\), where \(t\) represents the number of times noise is added. With various conditions, including the time step \(t\), text prompts \(c_t\), and a control condition \(c_f\), image diffusion algorithms learn a network \(ϵ_θ\) to predict the noise added to the noisy image \(z_t\).
This network is trained using the following formula:
\[L = \mathbb{E}_{z_{0,t},c_{t},c_{f},\epsilon \sim N(0,1)} [||\epsilon - \epsilon_{\theta}(z_{t}, t, c_{t}, c_{f})||^{2}_{2}]\]Here, \(L\) represents the overall learning objective of the entire diffusion model. This learning objective is used in fine-tuning diffusion models with ControlNet.
FreeControl
FreeControl introduces a comprehensive framework for zero-shot controllable T2I diffusion. It supports multiple control conditions (sketch, normal map, depth map, etc.), model architectures, and customized checkpoints without any training. Leveraging a pre-trained T2I diffusion model, denoted as \(ϵ_θ\), the framework integrates text prompts \(c\) and guidance images \(I_g\) to steer the image generation process. This ensures not only adherence to the provided text prompts but also the preservation of semantic structures outlined by the guidance images throughout the generation process.
Architecture
FreeControl comprises two stages: Analysis and synthesis. In the analysis stage, seed images for a target concept are generated, and semantic bases are extracted from them. In the synthesis stage, image synthesis occurs utilizing structure and appearance guidance.
Analysis Stage
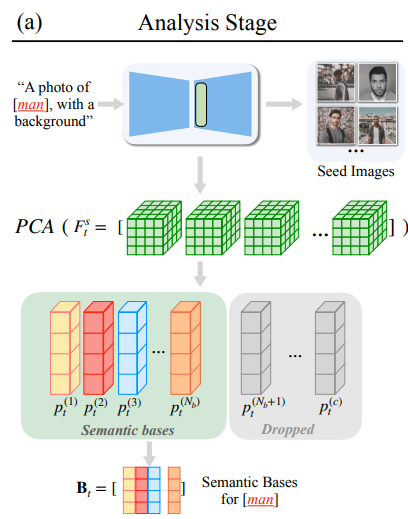
Fig 3. Analysis Stage [2].
In the pursuit of achieving robust semantic control in image generation, the concept of seed images is employed. This method initiates with the collection of a set of \(N_s\) images, denoted as \({I_s}\). These seed images are generated using the \(ϵ_θ\) model, employing a modified text prompt \(\tilde{c}\) derived from \(c\). \(\tilde{c}\) adds the concept tokens to a purposefully generic template, which enables \({I_s}\) to keep representations of semantic bases. (Suppose \(c\) is a man. \(\tilde{c}\) would be “A photo of [man] with background.”)
Next, DDIM inversion is applied on the set of seed images \({I_s}\) to derive time-dependent diffusion features \({F^t_s}\). Subsequently, Principal Component Analysis (PCA) is utilized on \({F^t_s}\) to extract time-dependent semantic bases \(B_t\). These \(B_t\) span semantic spaces \(S_t\), facilitating the propagation of image structure from the guidance image \(I_g\) to the synthesized image \(I\) during the synthesis stage.
\[B_t = [p^{(1)}_t, p^{(2)}_t, ..., p^{(N_b)}_t] ∼ PCA({F^s_t})\]Synthesis Stage
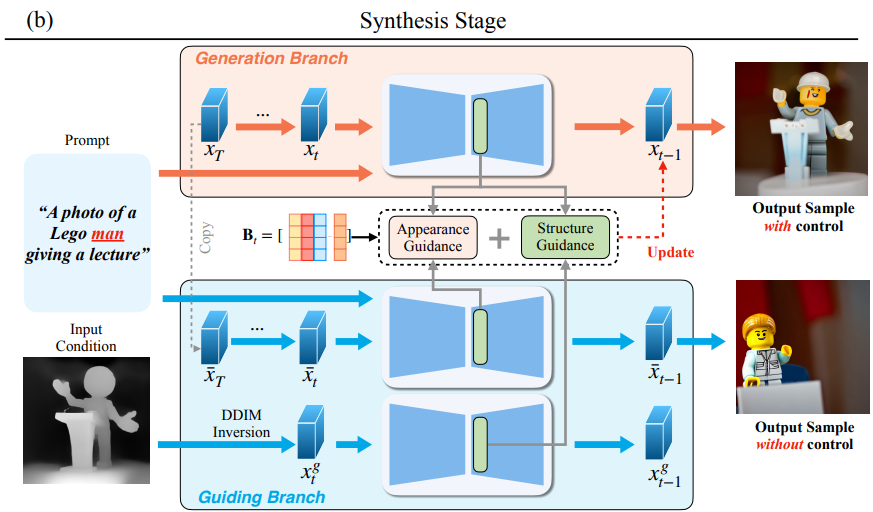
Fig 4. Synthesis Stage [2].
Initially, DDIM inversion is conducted on the guidance image \(I_g\) to acquire \(F^g_t\), subsequently projecting them onto \(B_t\) to determine their semantic coordinates \(S^g_t\). To achieve fine-grained control over foreground structure, a mask \(M\) is additionally generated using cross-attention maps of the concept tokens.
At each denoising step \(t\), the energy function gs for structure guidance is defined as follows:
\[g_{s}(S_{t}; S^{g}_{t},M) = \frac{\sum_{i,j} m_{ij} \lVert [s_{t}]_{ij} - [s^{g}_{t}]_{ij} \rVert^{2}_{2}}{\sum_{i,j} m_{ij}} + w \cdot \frac{\sum_{i,j} (1 - m_{ij}) \lVert \max([s_{t}]_{ij} - \tau_{t}, 0) \rVert^{2}_{2}}{\sum_{i,j} (1 - m_{ij})}\]where \(i\) and \(j\) are spatial indices for \(S_t\), \(S^g_t\) and \(M\), and \(w\) is the balancing weight.
The primary term aligns the structure of the synthesized image I with that of the guidance image \(I_g\), while the secondary term aids in delineating the foreground by suppressing spurious structures in the background.
Appearance guidance is applied to borrow texture from \(\overline{I}\), a sibling image of \(I\) generated without structure guidance. The appearance representation is as follows:
\[v^{(k)}_t = \frac{\sum_{i,j} \sigma([s^{(k)}_t]_{ij})[f_{t}]_{ij}}{\sum_{i,j} \sigma([s^{(k)}_t]_{ij})}\]The energy function ga for appearance guidance is as follows:
\[g_{a}(\{v^{(k)}_{t}\}; \{\bar{v}^{(k)}_{t}\}) = \frac{\sum_{k=1}^{N_a} \lVert v^{(k)}_{t} - \bar{v}^{(k)}_{t} \rVert^{2}_{2}}{N_a}\]Finally, the modified score estimate et includes structure and appearance guidance alongside classifier-free guidance.
\[\hat{\epsilon}_{t} = (1+s) \epsilon_{\theta}(x_{t};t, c) - s \epsilon_{\theta}(x_{t};t, \emptyset) + \lambda_{s} g_{s} + \lambda_{a} g_{a}\]Experiments
Our experimentation involved feeding Canny edge-detected images into both ControlNet and FreeControl pipelines. For ControlNet, we used the pretrained sd-controlnet-canny model alongside stable diffusion v1.5. Conversely, FreeControl was applied solely with stable diffusion v1.5.
ControlNet vs. FreeControl with a canny edge image
When the input condition and prompt align
| Condition | Value |
|---|---|
| Input Condition | A canny edge image of “Girl With A Pearl” |
| Prompt | “taylor swift, best quality, extremely detailed” |
| FreeControl text prompt | “A photo of a woman” |

Fig 5. ControlNet vs. FreeControl with a canny edge image: When the input condition and prompt align.
It shows that both ControlNet and FreeControl work decently when the input condition and prompt align.
When the input condition and prompt do not align
| Condition | Value |
|---|---|
| Input Condition | A canny edge image of dog |
| Prompt | “A 3d animation image of a lion, in the desert, best quality, extremely detailed” |
| FreeControl text prompt | “A photo of a dog” |

Fig 6.ControlNet vs. FreeControl with a canny edge image: When the input condition and prompt do not align.
It shows that ControlNet doesn’t work well when there is a conflict between the input condition and the prompt. However, FreeControl works well.
FreeControl semantic bases
| Condition | Value |
|---|---|
| Input Condition | A canny edge image of dog |
| Prompt | “A 3d animation image of a lion, in the desert, best quality, extremely detailed” |
| FreeControl text prompt | “A photo of a cat”, “A photo of a dog”, “A photo of a house” |

Fig 7.FreeControl semantic bases.
It shows that even the different text prompts have different bases, but all of them can generate images good enough.
Conclusion
The fundamental disparity that arises between ControlNet and FreeControl is the necessity of training. Unlike ControlNet, which mandates a training phase, FreeControl operates without such a prerequisite. However, it’s important to note that FreeControl incurs a significant increase in inference time compared to ControlNet. In empirical tests, ControlNet exhibited a runtime of 5.82 seconds. Conversely, FreeControl demanded a substantial duration of 95.5682 seconds for inversion and 100 seconds for generation. While the training phase for ControlNet consumes considerable time, its inference stage is efficient, with a notably shorter runtime. Both techniques have both advantages and drawbacks, underscoring the importance of selecting the appropriate one tailored to the model’s intended usage.
Code
ControlNet: ControlNet Colab
FreeControl: FreeControl GitHub
Demo: Colab
Reference
[1] Zhang, Rao, et al. “Adding Conditional Control to Text-to-Image Diffusion Models.” IEEE International Conference on Computer Vision. 2023.
[2] Mo, Mu, et al. “FreeControl: Training-Free Spatial Control of Any Text-to-Image Diffusion Model with Any Condition.” Computer Vision and Pattern Recognition. 2024.